Smartphones as a Tool for Measurement and Visualization in Physics Education
Authors: Ivelina Kotseva, Maya Gaydarova and
Authors information: |
|
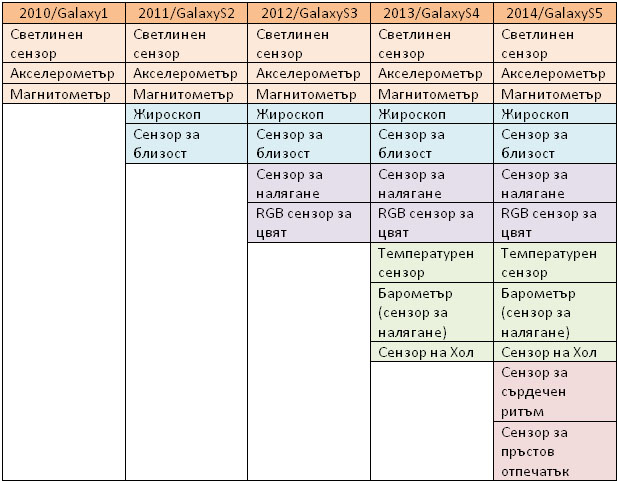
Фиг.1. Вграждане на сензори в Samsung Galaxy (хронологично представяне)(4)
По-съвременните смартфони притежават и сензори за влажност, температура, разстояние, светлина, сензор на Хол и др. Не са за подценяване и възможностите, които имат камерите, в които са вградени сензори, разработени на базата на съвременни иновативни технологии(5). Интересна експериментална установка за бета-спектроскопия, базирана на камера с вградени CMOS сензори и мобилното приложение RadioactivityCounter е описана от авторите Gröber et al. (2014). Също на камерата и вградените в нея CMOS сензори дължим изследвания, подобни на описаните от Whiteson et al. (2014) и Cogliati et al. (2014). Макар и да не се интересуваме пряко от техническите подробности, свързани със сензорите, някои автори съветват да се запознаем поне отчасти с принципното им устройство и действие (Countryman, 2014; Gallitto&Lupo, 2015; Kuhn&Vogt, 2013a; Silva, 2012; Vogt&Kuhn, 2012). Ще се ограничим само с акселерометъра поради по-големия брой експерименти, базирани на този сензор. Наличието на много сензори има и своята негативна страна– увеличаване разходът на енергия, който от страна на акселерометъра е значителен и се определя с необходимостта от непрекъснат достъп до данните на сензорите (Vanini et al., 2016).
Предназначение и принципно действие на акселерометъра
Акселерометърът е електромеханично устройство, измерващо ускорението в резултат на действащите сили, които могат да бъдат статични, като гравитационната сила на Земята, например, или динамични, т.е. водещи до преместване или вибрация на акселерометъра(6). Чрез измерване на ускорението, дължащо се на гравитацията, може да бъде изчислен ъгълът спрямо Земята, на който е завъртяно устройството, а чрез измерване на ускорението, дължащо се на динамични сили, може да се анализира движението на акселерометъра. Благодарение на тези функции на акселерометъра, смартфоните могат да обръщат ориентацията на екрана си в режим „портрет” или „пейзаж”, в зависимост от това как ги държим. Друго важно приложение намираме в лаптопите за автоматична защита на хард диска при рязко падане, както и при отваряне на въздушните възглавници в превозните средства при катастрофа.
Три са по-важните въпроси от методическа гледна точка при използването на акселерометъра като измервателно средство във физични експерименти (Countryman, 2014):
- Как могат да бъдат определени осите на смартфона, по които се отчитат трите компоненти на ускорението?
- Защо акселерометърът отчита ненулево ускорение, когато смартфонът е в стационарно положение?
- Как физическото положение и движение на устройството се преобразува в цифрови данни?
Преди всичко е необходимо да се инсталират съответните приложения, които позволяват достъп до данните на сензорите на смартфона, като SensorLog(7) (за iPhone) и AndroSensor(8) (за Android). За определяне на осите на смартфона, най-напред го завъртаме така, че долният ръб да опре вертикално на някаква плоскост, успоредна на земната повърхност (например на маса). На това положение отговарят показанията на акселерометъра на Фиг. 2а. При завъртане върху ръб по дължината на смартфона показанията отговарят на тези от Фиг. 2b и накрая, когато смартфонът е оставен върху плота на масата показанията са тези на Фиг. 2с. Тези показания варират за отделните смартфони, но като цяло имаме обща закономерност – във всяка една от трите позиции показанията по две от осите са приблизително 0, докато при третата показанието е приблизително 1g. По този начин определяме и осите (Kuhn&Vogt, 2013a).

|
Фиг.2. Скрийншот на показанията на AndroSensor при определяне
осите на смартфона
Фактът, че акселерометърът отчита ускорение с големина g, докато смартфонът е в стационарно положение е смущаващ за студентите и по естествен път води до дискусия относно механиката на акселерометъра, а от там и до принципа на еквивалентност на Айнщайн (Countryman, 2014; Kalotas&Wybourne, 1981). Можем да обясним принципа на действие на акселерометъра с модела на топче, окачено на пружина, свързана със скала с начало в центъра на топчето. Повдигайки пружината, тя ще се разпъне заради силата на тежестта, действаща на топчето и на скалата ще имаме показание -1g. Ако обратно, оставим пружината неподвижна (в хоризонтално положение), тя няма да се разпъне по оста у и показанието на скалата ще бъде 0. Акселерометърът се състои от три такива „пружинени скали”, ориентирани съответно по осите х, у и z. Промяната в позицията по трите оси може да бъде измерена чрез пиезорезистивни, пиезоелектрични или капацитивни методи. В повечето случаи се прилагат капацитивни методи (Фиг. 3).
|
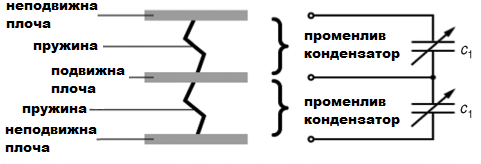
Фиг.3. Принцип на действие на акселерометъра (капацитивен метод)
Три силициеви плочи, разположени последователно и успоредно една на друга на равни разстояния са свързани с две пружини и с два променливи кондензатори. Двете външни плочи са фиксирани, а вътрешната е подвижна. Ускорението води до промяна в разстоянията между средната и външните плочи, което от своя страна води до промени в капацитетите на кондензаторите. Тези промени се измерват и преобразуват в стойности на ускорението (Vogt&Kuhn, 2012).
Приложение на смартфоните в механиката
Ще групираме приложенията на смартфоните в механиката в 5 основни категории:
- Опити в акустиката. Изучаване на ефекта на Доплер;
- Определяне на земното ускорение;
- Визуализация на явлението биене;
- Изучаване на въртеливи движения и определяне на ъгловото ускорение;
- Числен анализ на двойка осцилатори.
(1) Опити в акустиката. Изучаване на ефекта на Доплер
Акустиката е наука за звука, а той вълнува хората и предизвиква техния интерес още от зората на човешката история. Скоростта на звука във въздушна среда е предмет на сериозни научни дискусии от 17в. до 19в. Връзката между светлина и звук е в основата на първите опити за измерване на скоростта на звука (първо виждаме светкавицата, а после чуваме звука, което ни позволява, знаейки разстоянието и времето, за което звукът достига до нашето ухо, да изчислим скоростта му). Днес разполагаме с по-съвременни методи за определяне на тази скорост знаейки, че звукът е механична вълна с определена дължина λ и честота , чието произведение е точно равно на скоростта.
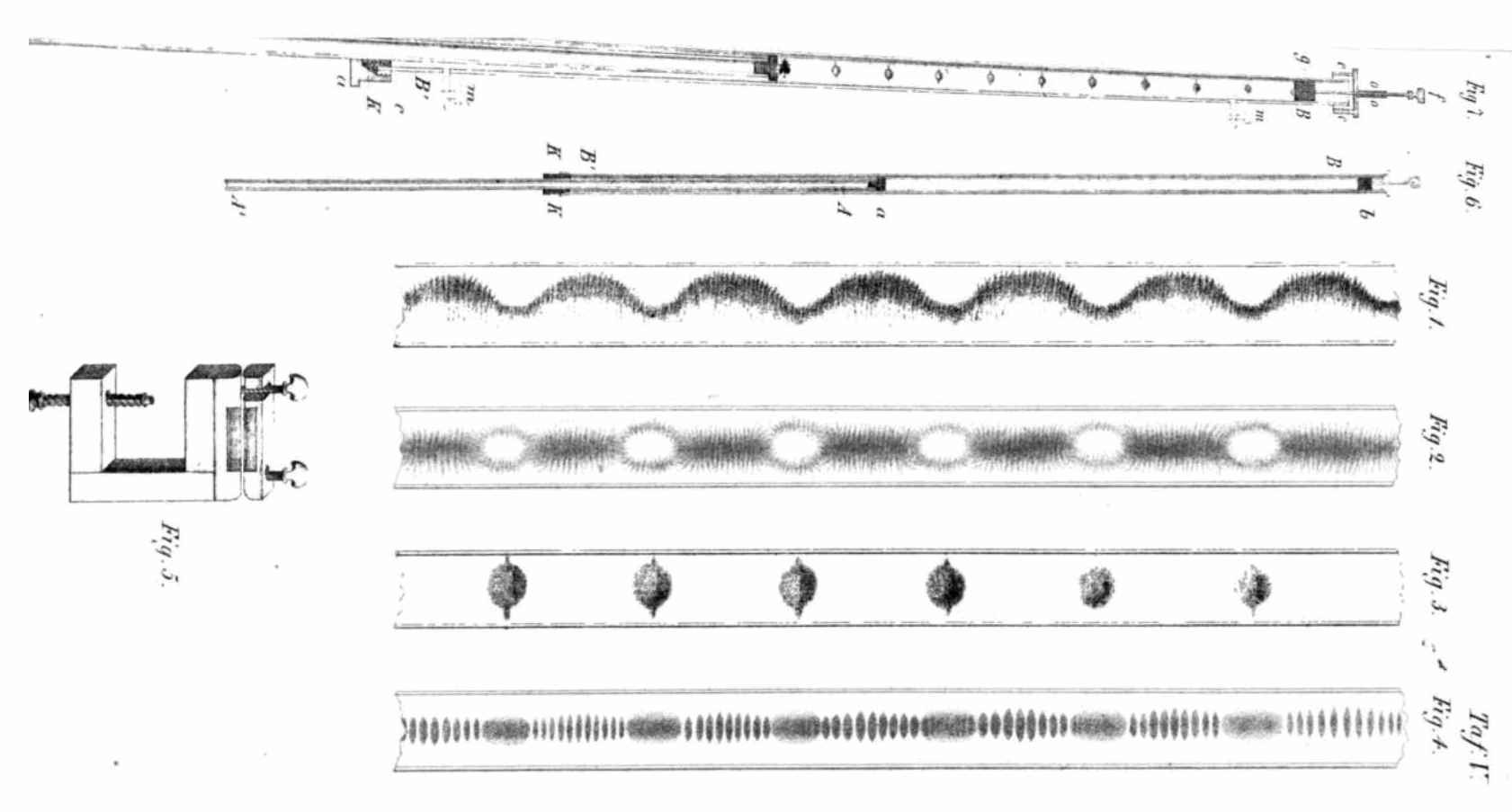
Един класически метод, който може да се използва и днес се състои в получаването на стоящи вълни в прозрачна хоризонтална тръба, затворена в единия край и съдържаща малко количество фин прах (например талк). За първи път методът е предложен през 1866 от немския физик August Kundt в така наречената тръба на Kundt (Фиг. 4). В отворения край се поставя източник на звук с постоянна честота (тон-генератор), а в другия край можем да скъсяваме или удължаваме тръбата, т.е. да регулираме нейната дължина докато звукът не стане внезапно по-силен, т.е докато не се получи резонанс. Това означава, че дължината на тръбата е кратна на половината от дължината на вълната на звука. В този момент в тръбата се е образувала стояща вълна.
|
Фиг.4. Рисунка от оригиналната статия на August Kundt, публикувана
в Annalen der Physik през 1866г(9).
Вместо тон-генератор (като емитер на звука) може да се използва смартфон с инсталирано приложение Function Generator(10). Втори смартфон е необходим (като колектор на звука) за отчитане честотата на стоящата вълна. Известно е, че всички смартфони притежават микрофони, с помощта на които могат да се записват звуци с честота до $44100\ \mathrm{Hz}$ (и дори до $48\ \mathrm{kHz}$ при по-съвременни модели). Това позволява да се изучават различни акустични явления с помощта на микрофона и множество свободно достъпни приложения (Audio Spectrum Monitor, Spectrum Analyzer и др.) за анализ на честотния спектър на звука. Прецизността, с която може да бъде измерена фундаменталната честота на звуковата вълна, позволява изучаването на честотната модулация на звука (Gómez‐Tejedor et al, 2015). Предложени са различни варианти на експеримента на Kundt - с тръба, отворена в двата края и тръба отворена в единия край и затворена в другия край (Parolin&Pezzi, 2015; Yavuz&Temiz, 2015). Трябва да се има предвид, че в първия случай фундаменталната честота ${f_0}$ на стоящата вълна (наречена още първа хармоника) се дава със зависимостта ${f_0} = {v/{(2L)}}$, където $v$ е скоростта на звука, а $L$ е дължината на тръбата. Във втория случай фундаменталната честота ${f_0}$ на стоящата вълна съответно се дава със зависимостта ${f_0} = {v/{(2L)}}$. Знаейки ${f_0}$ и $L$, намираме $v$.
Известно е, че скоростта на звука зависи от температурата и плътността на средата. Например, при $0\mathrm{^{\circ}C}$ скоростта във въздух е около $331\ \mathrm{m/s}$, в хелий е около $965\ \mathrm{m/s}$, а във въглероден диоксид е около $259\ \mathrm{m/s}$. Авторите Parolin&Pezzi (2013) ни запознават с интересни експерименти, при които с помощта на смартфони се измерват тези скорости в различни газови среди. Чрез използването на смартфони е възможно дори изучаването на акустичните и механичните свойства на метали (González et al., 2015; González&González, 2016).
Ефектът на Доплер при звукови вълни присъства всекидневно в живота ни. Klein et al. (2014) предлагат идея за неговото изучаване, отново базирана на използването на два смартфона – единият, прикрепен към въртящ се диск, се използва като източник на звук (емитер), а другият, който е стационарен, се използва като детектор. За целта, на първия смартфон, който ще служи за емитер, трябва да се инсталира приложение, което генерира звуци (напр. Function Generator за Android). Съответно, на смартфона, който ще изпълнява ролята на приемник на звука се инсталира друго приложение за отчитане и визуализация на параметрите на звука (напр. SPARKvue, AR-Osciloscope). Предимството на SPARKvue пред други приложения (напр. RealTimeSound), които също могат да бъдат използвани е, че позволява запаметяване и експортиране на данните във вид на .CSV файл (само в табличен, но не и в графичен вид). Подходящо е също платеното приложение Audio Kit.
Нека дискът, върху който е поставен емитерът се върти с постоянна скорост $u$. Честотата на излъчвания звук $f_e$ също е постоянна (напр. $19\ \mathrm{kHz}$). Честотата на звука $f_d$, която детекторът отчита е променлива, като максималната и минималната стойност (съответно $f_{d,max}$ и $f_{d,min}$) биват отчетени при двете диаметрално противоположни позиции на емитера върху въртящата се плоскост по правата, съединяваща детектора с центъра на диска. Това ни позволява да пресметнем скоростта на звука $v$, преработвайки формула (1) до формула (2)
| (1) | $$\Delta f = {f_d} - {f_e} = \pm {f_e}\frac{1}{{\frac{v}{u} \mp 1}}$$ |
| (2) | $$v = \frac{u}{{1 - \frac{{{f_e}}}{{{f_{d,max}}}}}} = \frac{u}{{\frac{{{f_e}}}{{{f_{d,min}}}} - 1}}$$ |
| (3) | $$u = \frac{{2\pi rn}}{t} = \frac{{2\pi r}}{T}$$ |
Според авторите на експеримента относителната грешка е приблизително $10%$ при абсолютна грешка $\Delta{f_{d,max}}=6\ \mathrm{Hz}$ и $\Delta{T}=0.01\ \mathrm{s}$, изчислено при $\Delta{t}=1\ \mathrm{s}$ за $n=100$ завъртания на диска.
Според Gómez-Tejedor et al. (2014) с ефект на Доплер и мобилни приложения могат да се изследват четири вида механични движения: равномерно линейно движение, равноускорително линейно движение, просто хармонично трептене и затихващо хармонично трептене. Главната идея е, че измерената промяна в честотата при Доплеровия ефект е свързана със скоростта на смартфон, поставен на количка, движеща се върху релса (при изучаване на първите две движения). За изучаване на хармонично трептене смартфонът се окачва вертикално на две еднакви пружини, закрепени неподвижно.
(2) Определяне на земното ускорение
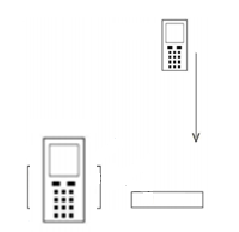
Kuhn&Vogt (2013a) предлагат различни методи за определяне на земното ускорение g с помощта на смартфони, включително и експеримент базиран на ефекта на Доплер (Kuhn&Vogt, 2013), който ще опишем. Нека свободно падащ смартфон (падащ върху мека повърхност, например възглавница) генерира звук с определана постоянна честота $f_0$ (Фиг. 5).
|
Фиг.5. Експериментална установка за определяне на земното ускорение $g$
Звукът се генерира с помощта на някое от посочените по-горе мобилни приложения. Друг смартфон изпълнява ролята на осцилоскоп. За целта използваме неговия микрофон и инсталираме съответното приложение (такива има много), например oScope Lite (за iOS) или AR-Osciloscope (за Android). Микрофонът на неподвижния смартфон трябва бъде разположен непосредстено на височината на мястото на падане на другия смартфон. Имаме следното добро приближение за Доплеровото отместване $\Delta{f}$.
| (4) | $$\Delta f \approx {f_0}\frac{v}{c}$$ |
| (5) | $$\Delta f \approx {f_0}\frac{{g\Delta t}}{c}$$ |
| (6) | $$g \approx \frac{{mc}}{{{f_0}}}$$ |
Друг метод за определяне на $g$ (чрез подскачаща топка и уравненията, описващи движението и) e предложен от Scwarz et al. (2013).
(3) Визуализация на явлението биене
Има достатъчно публикации, посветени на това явление, включително визуализацията му с помощта на смартфони (Ganci&Ganci, 2015; Keeports, 2015; Kuhn et al., 2014). Оказва се, че визуализация на явлението биене може да бъде постигната много лесно с помощта на 3 смартфона, разположени по начина, показан на Фиг. 6. (Kuhn&Vogt, 2013b).
|
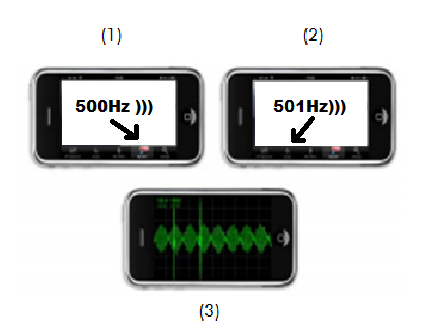
Фиг.6. Визуализация на явлението биене с помощта на 3 смартфона
За целта смартфони (1) и (2) трябва да генерират звуци (приложението Function Generator) с близки честоти, например $500\ \mathrm{Hz}$ и $501\ \mathrm{Hz}$ съответно. Смартфон (3) визуализира явлението чрез някое от приложенията AR-Osciloscope, RealTimePhysics или други.
Биене се получава и може също да бъде визуализирано в механични системи като системата „маса-пружина” или система от „свързани махала”. В първия случай (подробно описан в Giménez et al., 2017) към пружина, свързана с генератор на променлив ток, директно е окачен смартфон, чийто акселерометър служи за директна визуализация на биенето. Авторите подробно са извели математическите уравнения, описващи трептенето на системата при двата възможни варианта на този вид експерименти – на затихващо и на незатихващо трептене. Описан е и самият експеримент. Най-напред (при изключен генератор) се определя собствената честота $f_0$ на системата с помощта на приложението Accelerometer Monitor (за Android). Периодът $T_0$ на собствено трептене се определя графично и е $0.369\ \mathrm{s}$, откъдето $f_0=1/T_0=2.710\ \mathrm{Hz}$. След като сме определили собствената честота $f_0$ включваме генератора и настройваме честотата на принуденото трептене да бъде близка до $f_0$, например $f_0=2.769\ \mathrm{Hz}$ и $f_0=2.952\ \mathrm{Hz}$. Явлението биене и в двата случая бива визуализирано много добре. Пресметната грешка е малка (дори когато данните не са получени с изключително голяма прецизност, грешката е от порядъка на $2\%$).
Във втория случай, на две еднакви пружини са окачени два смартфона, като пружините са свързани чрез неразтегливи нишки с окачена тежест на равни височини и разстояния от двете пружини (Фиг. 7). Тъй като в българската литература не е отдадено достатъчно внимание на този експеримент, макар че той има много варианти, а освен това може да бъде много добре визуализиран с помощта на смартфони, ще приложим неговото по-подробно описание, както е представено то от авторите Kuhn&Vogt (2012). Ака едно от двете махала бъде приведено в движение, то неговото трептене скоро се предава на другото махало. Стига двете пружини да имат една и съща константа на еластичност, първото махало става неподвижно след известно време за кратко, като е предало цялата енергия на трептене на второто. От този момент нататък двете махала обменят тази енергия помежду си по този начин. Освен като окачени тежести на тези пружини, двата смартфони служат и като измервателни уреди, които записват данните от двете трептения. Бързината на обмяна на енергията между двете махала зависи от масата на окачената теглилка между двата смартфона (на Фиг. 7 тежестта е 100г).

|
Фиг.7. Експериментална установка на свързани махала
Едно от възможните усложнения при анализа на данните от този експеримент е синхронизацията на двете махала. Затова прилагаме следният метод: най-напред поотделно стартираме измерванията на двата смартфона. След като системата достигне равновесие, леко удряме стойката на окачване, което и в двете серии от данни се отбелязва ясно като пик. При анализа на данните времевите оси се транслират така, че този пик да се премести до началото. Подобни експерименти, в които смартфонът едновременно играе роля и на измервателно средство и на теглилка могат да послужат за определяне на коефициента на еластичност на пружина (Sans et al., 2017). Изследване на трептения могат да се направят и с помощта на светлинния сензор на смартфона (Sans et al., 2013).
(4) Изучаване на равномерни и равноускорителни въртеливи движения
Особено полезни са примерите във връзка с изучаване на въртеливите движения, в които с помощта на смартфона и други подръчни средства става възможно определянето на радиалното (центростремително) ускорение и ъгловата скорост, било чрез акселерометъра (Castro-Palacio, J. C. et al. (2014); Vogt& Kuhn, 2013), било чрез жироскопа (Pörn, R., & Braskén, M., 2016) на смартфона. Във всички случаи трябва да ползваме въртящ се диск (или греда/ летва) и мотор (с какъвто обикновено лабораториите по физика разполагат). Разгледан е случаят с равномерно движение. Измерването (стартиране на съответното приложение) започва преди включване на мотора, поради което на графиката, изобразяваща зависимостта на радиалното ускорение $a\ \mathrm{(m/s^2)}$ от времето $t\ \mathrm{(s)}$ съответства стойност $0\ \mathrm{m/s^2}$ до момента, в който не бъде включен мотора (около $5\ \mathrm{s}$ след стартиране на измерванията за по-ясно разграничение на данните върху графиката), което съответства на рязък пик върху същата графика. Правят се няколко измервания за различни интервали от време (например, $20$, $50$ и $80\ \mathrm{s}$). След това, получените резултати се съпоставят с теоретичните, получени от формулите (7), (8) и (9):
| (7) | $$a = \frac{{{v^2}}}{r} = \frac{{{n^2}4{\pi ^2}r}}{{{t^2}}}$$ |
| (8) | $$a = \frac{{{v^2}}}{r} = {\omega ^2}r$$ |
| (9) | $$\omega = \sqrt {\frac{a}{r}}$$ |
(5) Числен анализ на двойка осцилатори
Анализът на двойка осцилатори винаги е свързан със специално отношение в курсовете по физика, от една страна поради важността на тази физична система и от друга, поради сложността на математическия формализъм, свързан с нейното изучаване. Обикновено двойката осцилатори се представят чрез физичен експеримент, базиран на тела, окачени на пружини или махала. Експериментална постановка с участието на два смартфона с инсталирани приложения за разчитане на данните от акселерометрите им (необходим е и експорт на данните във вид на файл) е описана от авторите Castro-Palacio et al., 2013. Използвани са още три пружини с един и същи коефициент на еластичност $k_0$, два плъзгача, върху които хоризантално се закрепват смартфоните и релса, по която се движат плъзгачите. Коефициентът $k_0$ може да бъде определен предварително чрез измерване на отместването $x$ на пружината след окачване на тежест с маса m и на база на зависимостта (10):
| (10) | $$mg = {k_0}x$$ |
Масите на плъзгачите и съответните смартфони върху тях се изравняват с помощта на компенсаторни тежести до една и съща маса $m$. При такава система осцилациите са само по едната ос на смартфоните. Ускоренията $a_1$ и $a_2$ на двата смартфона се описват теоретично съответно от уравнения (11) и (12):
| (11) | $${a_1} = \frac{{{d^2}{x_1}}}{{d{t^2}}} = - \frac{1}{2}\left( {{A_1}{\omega _1}^2\sin \left( {{\omega _1}t + {\varphi _1}} \right) + {A_2}{\omega _2}^2\sin \left( {{\omega _2}t + {\varphi _2}} \right)} \right)$$ |
| (12) | $${a_2} = \frac{{{d^2}{x_2}}}{{d{t^2}}} = - \frac{1}{2}\left( {{A_1}{\omega _1}^2\sin \left( {{\omega _1}t + {\varphi _1}} \right) - {A_2}{\omega _2}^2\sin \left( {{\omega _2}t + {\varphi _2}} \right)} \right)$$ |
Следват описанията на три варианта на експеримента:
- При еднакво първоначално отместване на двата плъзгача в една и съща посока (тогава ${A_2} = 0$);
- При еднакво първоначално отместване на двата плъзгача, но в различни посоки (тогава ${A_1} = 0$);
- При първоначално отместване само на единия от плъзгачите и оставане в равновесно положение на другия плъзгач.
И в трите варианта параметрите са получени по алгоритъма на Levenberg-Marquardt за апроксимиране по метода на най-малките квадрати на налинейни параметри и с помощта на програмата ORIGIN ver 6.1 (Castro-Palacio et al., 2013).
Подобно на двойката осцилатори, изучаването на двумерен осцилатор също бива улеснено с помощта на два смартфона. Интересен случай, в който биват визуализирани и фигури на Лисажу са дали авторите Tuset-Sanchis et al., 2015.
Приложение на магнитометъра на смартфона
С помощта на магнитометъра на един смартфон могат да бъдат измервани матнитните полета на малки магнити (Arribas et al., 2015) или да бъде изучавано магнитното поле на Земята (Arabasi&Al-Taani, 2016). Данните от магнитометъра на смартфона могат да бъдат използвани и при анализирането на хармонични движения (Yavuz&Temiz, 2016) или при измерването на кинематични променливи (Temiz& Yavuz, 2015). Ако сме решили да използваме магнитометъра на смартфона си при физични експерименти и демонстрации трябва да знаем преди всичко, че силните магнити, респ. магнитни полета могат да го повредят. От друга страна е важно да знаем къде точно е разположен магнитометъра на нашия смартфон, което се установява по следния начин (Ogawara et al., 2017). Най-напред, разбира се, инсталираме някакво приложение за разчитане на данните (такива има много), например Sensor Box for Android (play.google.com/store/apps), след което движейки смартфона над някакъв много слаб магнит или слабо намагнетизирано желязо определяме позицията, в която приложението отчита най-висока стойност на магнитната индукция. Магнитометърът на смартфона се намира точно над магнита (желязото) в тази позиция. Знаейки местоположението на магнитометъра в нашия смартфон можем да демонстрираме опита на Оерстед чрез опъване на проводник над магнитомера, по който пускаме слаб ток. Имаме възможност да изучаваме магнитното поле на кръгов проводник (Ogawara et al., 2017) или пък промените в магнитното поле на соленоид в зависимост от броя на намотките (Silva, 2012), както и промените в магнитното поле на прав проводник, по който тече ток, в зависимост от разстоянието до проводника.
Заключение
Цитираните експерименти са прости, но напълно достъпни и особено полезни там, където не достига лабораторно оборудване. Те демонстрират само малка част от възможностите, които смартфоните и съответните мобилни приложения потенциално притежават при интегрирането им във физични експерименти и демонстрации. В заключение може да добавим и факта, че учениците повишават своята мотивация при изучаване на физиката, ако в обучението се отделя време и за експерименти, включително и такива, базирани на съвременни технологии, каквито са мобилните.
Тази публикация е осъществена с финансовата помощ на ФНИ към СУ„Св. Климент Охридски” по договор № 80.10-10/12.04.2017.
Notes
- https://www.aapt.org/Resources/iPhysics-Labs.cfm

- https://www.physik.uni-kl.de/iphysicslab/home/

- http://www.science-on-stage.eu/page/display/5/5/1290/istage-2-smartphones-in-science-teaching

- http://loganzone.buzingaapps.netdna-cdn.com/wp-content/uploads/2015/08/Sensor-growth-in-smartphones.jpg

- http://www.digital.bg/kakvo-predstavlqvat-novite-kamera-senzori-za-smartfoni-samsung-isocell-article601147.html

- https://www.dimensionengineering.com/info/accelerometers

- https://itunes.apple.com/us/app/sensorlog

- https://play.google.com/store/apps/details?id=com.fivasim.androsensor

- https://en.wikipedia.org/wiki/Kundt%27s_tube

- https://play.google.com/store/apps/details?id=com.keuwl.functiongenerator

References
- Arabasi, S., & Al-Taani, H. (2016). Measuring the Earth’s magnetic field dip angle using a smartphone-aided setup: a simple experiment for introductory physics laboratories. European Journal of Physics, 38(2), 025201.
- Arribas, E., Escobar, I., Suarez, C. P., Najera, A., & Beléndez, A. (2015). Measurement of the magnetic field of small magnets with a smartphone: a very economical laboratory practice for introductory physics courses. European Journal of Physics, 36(6), 065002.
- Barrera-Garrido, A. (2015). Analyzing planetary transits with a smartphone. The Physics Teacher, 53(3), 179-181.
- Briggle, J. (2013). Analysis of pendulum period with an iPod touch/iPhone. Physics Education, 48(3), 285.
- Cabeza, C., Rubido, N., & Martí, A. C. (2014). Learning physics in a water park. Physics Education, 49(2), 187.
- Castro-Palacio, J. C., Velázquez-Abad, L., Giménez, F., & Monsoriu, J. A. (2013). A quantitative analysis of coupled oscillations using mobile accelerometer sensors. European Journal of Physics, 34(3), 737.
- Castro-Palacio, J. C., Velazquez, L., Gómez-Tejedor, J. A., Manjón, F. J., & Monsoriu, J. A. (2014). Using a smartphone acceleration sensor to study uniform and uniformly accelerated circular motions. Revista Brasileira de Ensino de Física, 36(2), 1-5.
- Cogliati, J. J., Derr, K. W., & Wharton, J. (2014). Using CMOS sensors in a cellphone for gamma detection and classification. arXiv preprint arXiv:1401.0766.
- Countryman, C. L. (2014). Familiarizing Students with the Basics of a Smartphone's Internal Sensors. The Physics Teacher, 52(9), 557-559.
- Forinash, K., & Wisman, R. F. (2012). Smartphones as portable oscilloscopes for physics labs. The Physics Teacher, 50(4), 242-243.
- Gabriel, P., & Backhaus, U. (2013). Kinematics with the assistance of smartphones: Measuring data via GPS-Visualizing data with Google Earth. The Physics Teacher, 51(4), 246-247.
- Gallitto, A. A., & Lupo, L. (2015). A mechanical model of the smartphone’s accelerometer. Physics Education, 50(6), 646.
- Ganci, A., & Ganci, S. (2015). The Simplest Demonstration on Acoustic Beats. The Physics Teacher, 53(1), 32-33.
- Giménez, M. H., Salinas, I., Monsoriu, J. A., & Castro-Palacio, J. C. (2017). Direct visualization of mechanical beats by means of an oscillating smartphone. The Physics Teacher, 55(7), 424-425.
- Gómez-Tejedor, J. A., Castro-Palacio, J. C., & Monsoriu, J. A. (2014). The acoustic Doppler effect applied to the study of linear motions. European Journal of Physics, 35(2), 025006.
- Gómez‐Tejedor, J. A., Castro‐Palacio, J. C., & Monsoriu, J. A. (2015). Frequency analyser: A new Android application for high precision frequency measurement. Computer Applications in Engineering Education, 23(3), 471-476.
- González, M. Á., & González Rebollo, M. Á. (2015). Physics in your pocket: experimenting and learning with your smartphone. Retrieved on 1st of November, 2017 from [https://uvadoc.uva.es/bitstream/10324/11893/7/MPTL_2015_submission_2_BO_editGonzalez.pdf]
- González, M. Á., da Silva, J. B., Cañedo, J. C., Huete, F., Martínez, Ó., Esteban, D., ... & González, M. Á. (2015, October). Doing physics experiments and learning with smartphones. In Proceedings of the 3rd International Conference on Technological Ecosystems for Enhancing Multiculturality (pp. 303-310). ACM.
- González, M. Á., & González, M. Á. (2016). Smartphones as experimental tools to measure acoustical and mechanical properties of vibrating rods. European Journal of Physics, 37(4), 045701.
- Gröber, S., Molz, A., & Kuhn, J. (2014). Using smartphones and tablet PCs for β−-spectroscopy in an educational experimental setup. European Journal of Physics, 35(6), 065001.
- Igoe, D., Parisi, A., & Carter, B. (2013). Smartphones as tools for delivering sun-smart education to students. Teaching Science, 59(1), 36.
- Igoe, D. P., & Parisi, A. V. (2015). Solar current output as a function of sun elevation: students as toolmakers. Physics Education, 50(6), 657.
- Kalotas, T. M., & Wybourne, B. G. (1981). An application of the equivalence principle in classical mechanics. European Journal of Physics, 2(1), 52.
- Keeports, D. (2015). Watching harmonics beat. The Physics Teacher, 53(4), 244-244.
- Klein, P., Hirth, M., Gröber, S., Kuhn, J., & Müller, A. (2014). Classical experiments revisited: smartphones and tablet PCs as experimental tools in acoustics and optics. Physics Education, 49(4), 412.
- Kuhn, J., & Vogt, P. (2012). Analyzing spring pendulum phenomena with a smart-phone acceleration sensor. The Physics Teacher, 50(8), 504-505.
- Kuhn, J., & Vogt, P. (2013a). Smartphones as experimental tools: Different methods to determine the gravitational acceleration in classroom physics by using everyday devices. European Journal of Physics Education, 4(1).
- Kuhn, J., & Vogt, P. (2013b). Applications and examples of experiments with mobile phones and smartphones in physics lessons. Frontiers in Sensors, 1(4), 67-73.
- Kuhn, J., Vogt, P., & Hirth, M. (2014). Analyzing the acoustic beat with mobile devices. The Physics Teacher, 52(4), 248-249.
- Kundt, A. (1866). Ueber eine neue Art Akustischer Staubfiguren und über die Anwendung derselben zur Bestimmung der Shallgeschwindigkeit in festen Körpern und Gasen. Annalen der Physik (in German). Leipzig: J. C. Poggendorff. 127 (4): 497–523.
- Löfstrand, M., & Pendrill, A. M. (2016). Aerodynamics in the amusement park: interpreting sensor data for acceleration and rotation. Physics Education, 51(5), 055015.
- Monteiro, M., & Martí, A. C. (2016). Using smartphone pressure sensors to measure vertical velocities of elevators, stairways, and drones. Physics Education, 52(1), 015010.
- Ogawara, Y., Bhari, S., & Mahrley, S. (2017). Observation of the magnetic field using a smartphone. The Physics Teacher, 55(3), 184-185.
- Parolin, S. O., & Pezzi, G. (2013). Smartphone-aided measurements of the speed of sound in different gaseous mixtures. The Physics Teacher, 51(8), 508-509.
- Parolin, S. O., & Pezzi, G. (2015). Kundt’s tube experiment using smartphones. Physics Education, 50(4), 443.
- Pendrill, A. M. (2015). Rotating swings—a theme with variations. Physics Education, 51(1), 015014.
- Polak, R. D., Fudala, N., Rothchild, J. T., Weiss, S. E., & Zelek, M. (2016). Easily accessible experiments demonstrating interference. The Physics Teacher, 54(2), 120-121.
- Pörn, R., & Braskén, M. (2016). Interactive modeling activities in the classroom—rotational motion and smartphone gyroscopes. Physics Education, 51(6), 065021.
- Puttharugsa, C., Khemmani, S., Utayarat, P., & Luangtip, W. (2016). Investigation of the rolling motion of a hollow cylinder using a smartphone. European Journal of Physics, 37(5), 055004.
- Sans, J. A., Manjón, F. J., Pereira, A. L. J., Gomez-Tejedor, J. A., & Monsoriu, J. A. (2013). Oscillations studied with the smartphone ambient light sensor. European Journal of Physics, 34(6), 1349.
- Sans, J. A., Manjón, F. J., Cuenca-Gotor, V., Giménez-Valentín, M. H., Salinas, I., Barreiro, J. J., ... & Gomez-Tejedor, J. A. Smartphone: a new device for teaching Physics. Downloaded from [http://ocs.editorial.upv.es/index.php/HEAD/HEAD15/paper/ viewFile/332/211] on 20th of September, 2017.
- Satoh, F., Sakagami, K., & Omoto, A. (2016). Application of a smartphone for introductory teaching of sound environment: Validation of the precision of the devices and examples of students' work. Acoustical Science and Technology, 37(4), 165-172.
- Schwarz, O., Vogt, P., & Kuhn, J. (2013). Acoustic measurements of bouncing balls and the determination of gravitational acceleration. The Physics Teacher, 51(5), 312-313.
- Shakur, A., & Kraft, J. (2016). Measurement of Coriolis acceleration with a smartphone. The Physics Teacher, 54(5), 288-290.
- Sharples, M., Taylor, J., & Vavoula, G. (2005, October). Towards a theory of mobile learning. In Proceedings of mLearn (Vol. 1, No. 1, pp. 1-9).
- Silva, N. (2012). Magnetic field sensor. The Physics Teacher, 50(6), 372-373.
- Streepey, J. W. (2013). Using iPads to illustrate the impulse-momentum relationship. The Physics Teacher, 51(1), 54-55.
- Temiz, B. K., & Yavuz, A. (2015). Magnetogate: using an iPhone magnetometer for measuring kinematic variables. Physics Education, 51(1), 015004.
- Testoni, L. A., & Brockington, G. (2016). The use of smartphones to teach kinematics: an inexpensive activity. Physics Education, 51(6), 063008.
- Tornaría, F., Monteiro, M., & Marti, A. C. (2014). Understanding coffee spills using a smartphone. The Physics Teacher, 52(8), 502-503.
- Tuset-Sanchis, L., Castro-Palacio, J. C., Gómez-Tejedor, J. A., Manjón, F. J., & Monsoriu, J. A. (2015). The study of two-dimensional oscillations using a smartphone acceleration sensor: example of Lissajous curves. Physics Education, 50(5), 580.
- Vanini, S., Faraci, F., Ferrari, A., & Giordano, S. (2016). Using barometric pressure data to recognize vertical displacement activities on smartphones. Computer Communications, 87, 37-48.
- Vieyra, R. E., Vieyra, C., & Macchia, S. (2017). Kitchen Physics: Lessons in Fluid Pressure and Error Analysis. The Physics Teacher, 55(2), 87-90.
- Vogt, P., & Kuhn, J. (2012). Analyzing free fall with a smartphone acceleration sensor. The Physics Teacher, 50(3), 182-183.
- Vogt, P., & Kuhn, J. (2013). Analyzing radial acceleration with a smartphone acceleration sensor. The Physics Teacher, 51(3), 182-183.
- Yavuz, A., & Temiz, B. K. (2015). Detecting interferences with iOS applications to measure speed of sound. Physics Education, 51(1), 015009.
- Yavuz, A., & Temiz, B. K. (2016). Analysing harmonic motions with an iPhone’s magnetometer. Physics Education, 51(3), 035006.
- Whiteson, D., Mulhearn, M., Shimmin, C., Cranmer, K., Brodie, K., & Burns, D. (2014). Observing ultra-high energy cosmic rays with smartphones. arXiv preprint arXiv:1410.2895.
 iva_georgieva
iva_georgieva phys.uni-sofia.bg
phys.uni-sofia.bg